Home > Project > Economy&Business > Automatical Trading and Cryptocurrency > Derivative Mathematical Pricing
Plain Vanilla
I took the related exercising for this pricing [here](https://colab.research.google.com/drive/18y8GSmrwECzgv3c385CnVVefUjEXtWaj?usp=sharing).2. Barrier Option Return Strategy
It’s a type of exotic option where the payoff depends on whether the underlying asset’s price reaches a certain level, or barrier, during its life. For this internship exercise, here I will cover the mathematical Principles, for detailed algorithm structure, refer to my GitHub Repository
Github: https://github.com/Viiiikedy/Barrier-option-returns-issue
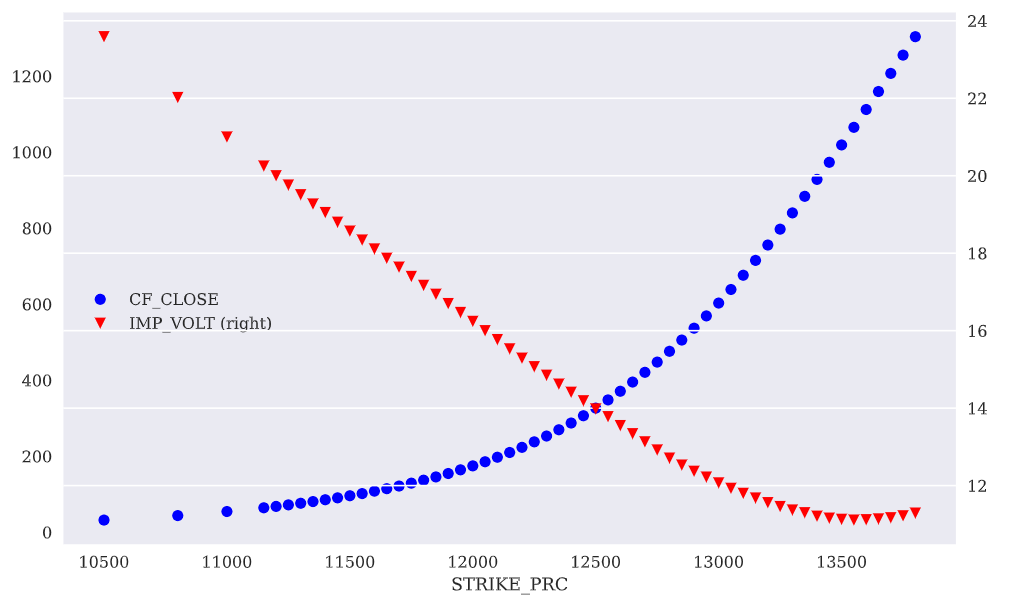
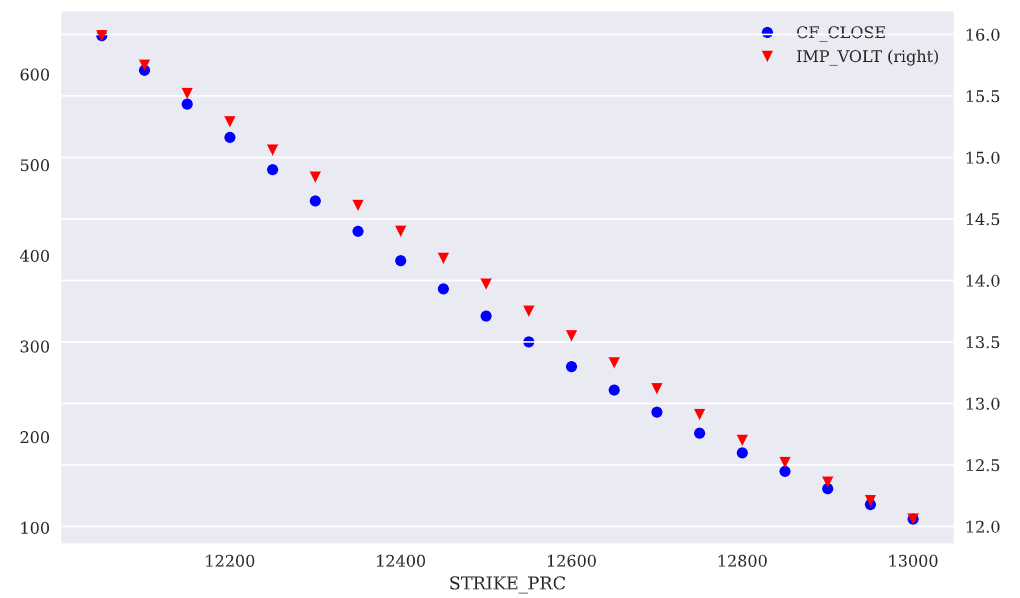
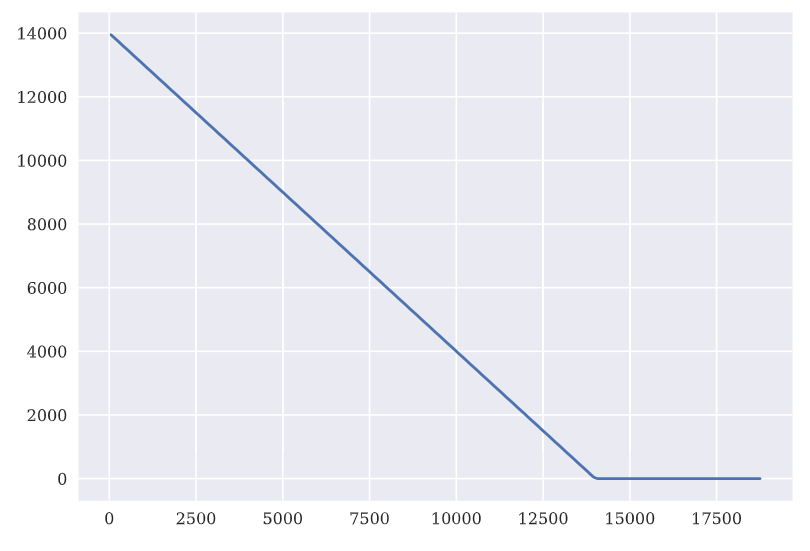
2.1 Basic Steps for Exotic Option Pricing
- Start with some financial product
- Model asset prices involved (SDEs)
- Calibrate the model to market data (numerics, optimization)
- Model product price correspondingly (P(I)DE or integral)
- Price the derivative product of interest (numerics, MC)
- Set up a hedge to remove the risk to the derivative product (optimization)
2.2 Mathematical Deduction
European Down and In Call (Under the condition of GBM) \[ c = S \exp^{-q(T-t)} \left( \frac{H}{S} \right)^{2 \lambda} N(y) - X \exp^{-r(T-t)} \left( \frac{H}{S} \right)^{2 \lambda - 2} N(y - \sigma \sqrt{T-t}) \] European Up and In Put: $$ p=X\exp^{-r(T-t)}(H/S)^{2\lambda-2}N(-y+\sigma \sqrt{T-t}) - S \exp^{-q(T-t)}(H/S)^{2\lambda}N(-y) $$
whereas r is market return, q is dividend rate and r_f is risk free rate. And:
$$
\lambda = \frac{r-r_f+\sigma^2/2}{\sigma^2}
$$
$$
y = \frac{\log{[H^2/(SX)]}}{\sigma \sqrt{T-t}} + \lambda \sigma \sqrt{T-t}
$$
Theorem
Down: H < S
Up: H>S
For the original case, S < K < H, up and in put option the formula is:
$$
p=K\exp^{-r(T-t)}(H/S)^{2\lambda-2}N(-y+\sigma \sqrt{T-t}) - S \exp^{-q(T-t)}(H/S)^{2\lambda}N(-y)
$$
using the common formalism. If we assume the underlying asset does not pay dividends we can a simplification:
$$
p=K\exp^{-r(T-t)}(H/S_0)^{2\lambda-2}N(-y+\sigma \sqrt{T-t}) - S_0 (H/S_0)^{2\lambda}N(-y)
$$
where
$$
\lambda = \frac{r+\sigma^2/2}{\sigma^2}
$$
$$
y = \frac{\log{[H^2/(S_0K)]}}{\sigma \sqrt{T-t}} + \lambda \sigma \sqrt{T-t}
$$
We will do Jump Diffusion model
$$
dS_t = (r-r_J)S_t dt + \sigma S_t dZ_t +J_tS_tdN_t
$$
Here, S_t is the spot price at t; r_t is constant short rate; r_J is drift correction term of the jump; Z_t Wiener process; J_t jump magnitude, it follows a normal distribution of $$N(\mu, \delta^2)$$ N_t is Poisson process $$\sim P(\lambda)$$
Needless to say, the Poisson process isn’t correlated with the Wiener process. To simulate such a price dynamic, the Euler discretization:
$$
S_t = S_{t-\Delta t}\Big( e^{(r-r_J-\sigma^2/2)\Delta t+\sigma \sqrt{\Delta t}z_t^1}+\Big(e^{\mu_J+\delta z_t^2}-1\Big)\Big)
$$
$$
r_J \equiv \lambda\Big(e^{\mu_J+\delta^2/2}-1\Big)
$$
3. Extension
You could aslo refer to my tutorial where I introduced more based on the most classical books in the financial engineering.
